أصبح الذكاء الاصطناعي في كل مكانٍ من حولنا: يقوم يوتيوب باقتراح فيديوهاتٍ جديدة علينا اعتماداً على تاريخ المشاهدة الخاص بنا ونوعية الفيديوهات التي نشاهدها؛ وذلك عبر خوارزميةٍ ذكية تقوم باستمرار بحساب الاقتراحات الممكنة، وهو الأمر نفسه الذي يقوم به فيسبوك من أجل عرض القصص والأخبار على صفحة نيوز فيد، فضلاً عن خوارزميته الذكية للتعرف على الأشخاص ضمن الصور. تعتمد المساعدات الرقمية الذكية مثل أليكسا وسيري وجوجل أسيستنت على برمجيات الذكاء الاصطناعي للتعرف على الأوامر الصوتية التي نُمليها عليها، وهو ما يمكنها من تنفيذ ما يتم طلبه منها. ببساطة: الأمثلة لا تنتهي، يمكن الحديث مطولاً عن أثر الذكاء الاصطناعي في كل المجالات التي تحيط بنا، من التواصل الاجتماعيّ وصولاً لأنظمة التشخيص المرضي في المستشفيات.
ولكننا نعلم أن الذكاء الاصطناعي نفسه هو توصيف لنمطٍ من البرمجيات الحاسوبية الذكية، ولا يمثل خوارزميةً بحد ذاتها؛ فهنالك العديد من الطرق التي يمكن استخدامها لإعطاء الآلة صفة "الذكاء". في السنوات الأخيرة، تزايد استخدام مُصطلح الشبكات العصبونية الاصطناعية (Artificial Neural Networks) عند الحديث عن تطبيقات الذكاء الاصطناعيّ في شتى المجالات، إلى الدرجة التي أصبحت فيها الشبكات العصبونية تعني الذكاء الاصطناعيّ عند الكثيرين، وهو أمرٌ غير دقيق؛ إذ إن الشبكات العصبونية تندرج فعلياً تحت مصطلح التعلم العميق الذي يعتبر أحد أشكال التعلم الآلي، وهو بدوره أحد فروع الذكاء الاصطناعي.
ما هي الشبكات العصبونية الاصطناعية؟
الشبكات العصبونية الاصطناعية عبارة عن برامج أو أنظمة حاسوبية تعتمد من حيث المبدأ على محاكاة عمل عصبونات الدماغ من أجل معالجة البيانات وإنجاز مهامٍ في مجالاتٍ متنوعة، وهي أشهر أنماط وطرق التعلم الآلي الهادف لتوفير خوارزمياتٍ وبرمجياتٍ قادرة على التعلم بالخبرة. عندما يتم القول إن الشبكات العصبونية تحاكي آلية عمل العصبونات الحيوية في الدماغ فهذا يعني أمرين: الأول بنيوي معني بتشكيل الشبكة العصبونية لتتكون من عددٍ معينٍ من العقد تُدعى كل منها "عصبون" مرتبطة مع بعضها البعض عبر وصلاتٍ اصطناعية. والأمر الثاني هو الناحية السلوكية؛ أي أن العصبونات الاصطناعية تقلد العصبونات الحيوية في كيفية توليدها للإشارات ونقلها فيما بينها، كما أن الشبكة العصبونية ككل يجب أن تحاكي عمل الدماغ من حيث قدرته على التعلم من الخبرة، وكلما ازدادت الخبرة المكتسبة ازدادت قوة المشابك بين العصبونات الحيوية، وبالتالي يصير أداؤنا في تنفيذ مهمةٍ ما أفضل. هذا الأمر نفسه يجب أن ينطبق على الشبكات العصبونية الاصطناعية.
مكونات الشبكات العصبونية الاصطناعية
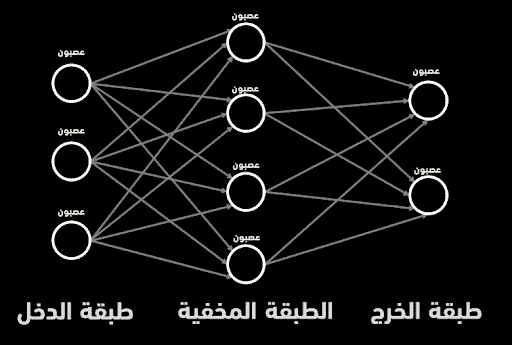
من حيث الشكل العام، تأخذ الشبكة العصبونية شكل طبقاتٍ متعددة تمتلك كل طبقة منها عدداً معيناً من العصبونات، وأقل عدد ممكن من الطبقات هو ثلاث: طبقة الدخل وطبقة الخرج والطبقة (أو الطبقات) المخفية. تقوم طبقة الدخل باستقبال البيانات التي يجب معالجتها، وبحسب قيم بيانات الدخل سيتم تفعيل عصبونات معينة ضمن طبقة الدخل، التي بدورها ستقوم بتفعيل عصبونات الطبقة المخفية، وهكذا وصولاً حتى طبقة الخرج التي نحصل من خلالها على القرار المتعلق بالمهمة المراد إنجازها.
تتألف الشبكة العصبونية من عصبونات مرتبة ضمن طبقات، بحيث يتصل كل عصبون في كل طبقة مع عصبونات الطبقة السابقة والتالية.
قد يهمك أيضاً:
كيف تعمل الشبكة العصبونية الاصطناعية؟
قد يكون من المفاجئ هذا القول، ولكن الشبكة العصبونية -بعيداً عن المصطلحات المعقدة- عبارة عن شبكة من الحسابات والتوابع الرياضية، وذلك بدءاً من الوحدة الأساسية التي تشكل الشبكة، أي العصبون، الذي يتم تشكيله فعلياً عبر تابعٍ رياضيّ يقوم بحساب قيمةٍ معينة.
من أجل فهم آلية عمل الشبكة العصبونية ككل، سيكون من المفيد أخذ مثالٍ شهير يوضح ذلك: برنامج حاسوبي مبني على شبكة عصبونيةٍ من أجل التعرف على الأرقام المكتوبة بخط اليد، وهي عادةً المهمة التي نستطيع إنجازها كبشر بشكلٍ بديهيّ؛ وذلك لأن دماغنا قد تدرب لفترةٍ طويلة على تمييز أنماط الكتابة وتفسيرها بشكلٍ ممتاز. بالنسبة للحاسوب فإن الأمر مختلف: يجب أن يتعلم أولاً ما هي الأرقام وأنماط كتابتها المعيارية، ومن ثم يجب أن يستطيع تعلم كيفية تفسير الأرقام المكتوبة بخط اليد وربط شكلها بالأنماط التي يعرفها سابقاً. وهذا فيديو ممتاز حول هذا المثال:
مصدر الفيديو: قناة (3Blue1Brown) على يوتيوب
ولننظر مثلاً لرقمٍ مثل 8، كيف يمكن أن نقوم بتحليله؟ يمكننا ذلك باعتبار أنه عبارة عن دائرتين متوضعتين فوق بعضهما البعض. ماذا عن الرقم 4؟ يمكن اعتبار أنه عبارة عن ثلاثة خطوط مستقيمة متقاطعة، أو اعتبار الرقم 9 أنه دائرة ذات خط منحنى يبدأ من جانبها. عندما ننظر إلى الأرقام اليوم لا نفكر فيها على هذا النحو، ولكن في لحظةٍ ما عند بداية تعلمنا للأرقام وتمييز أشكالها، قام دماغنا ببناء ترابطاتٍ بين الأشكال المختلفة وتدرب على كيفية فهمها وتفسيرها على أنها أرقام، وكلما قرأنا أكثر ازدادت قدرة دماغنا على التفسير السريع والفهم الفوريّ لمعنى الشكل المكتوب.
نريد أن نقوم ببناء شبكةٍ عصبونية تستطيع فعل ذلك، أي أن ندخل لها صورة رقم مكتوب بخط اليد وتستطيع الشبكة التعرف على الرقم الموجود في الصورة. يمكن تنفيذ ذلك عبر تشكيل شبكةٍ عصبونية تتكون من 4 طبقات: طبقة دخل تقوم باستقبال بيانات الصورة التي تتضمن الرقم، وبالتالي فإن عدد عصبونات هذه الطبقة سيساوي عدد البكسلات الموجودة في صورة الدخل، وإذا كان لدينا صورة تتضمن 784 بيكسل (أي 28*28) فهذا يعني أن طبقة الدخل ستمتلك 784 عصبون، وطبقتين مخفيتين تقوم الأولى بالتعرف على الأنماط الدقيقة (مثل الأقواس والمنحنيات الصغيرة) والثانية تقوم بالتعرف على الأنماط الكبيرة التي يمكن تشكيلها من الأنماط الدقيقة المكتشفة في الطبقة المخفية الأولى (الدائرة عبارة عن 4 أقواس على سبيل المثال)، وطبقة الخرج التي تتكون من 10 عصبونات، يمثل كل منها رقماً من 0 وحتى 9.
ما يجب أن يحدث ببساطة هو أننا سندخل صورة رقمية تتضمن رقماً مكتوباً بخط اليد، وسنعرف ما هو الرقم عبر العصبون ذي الاحتمالية الأعلى في طبقة الخرج والموافق لرقمٍ ما. كمثال، لو أدخلنا صورة تتضمن الرقم 3 مكتوباً بخط اليد، فستكون النتيجة أن كل عصبونات طبقة الخرج تمتلك احتماليةً معينة بين 0 و 100%، وسنجد أن العصبون الموافق للرقم 3 يمتلك أعلى احتمالية وهي 95%، وبالتالي ستعرف الشبكة أن الرقم الموجود في الصورة يمثل الرقم 3.
ما الذي يحدث ضمن هذه الشبكة؟ لنعد قليلاً للعصبونات: العصبون نفسه عبارة عن تابع رياضي يقوم بحساب قيمة تدعى: التفعيل (Activation)، وهذا يعني أن كل عصبون يمتلك قيمة تفعيل خاصة به، وحساب هذه القيمة يعتمد على قيم تفعيل العصبونات المرتبطة به وعلى قوة تشابكه معها. كيف نحسب "قوة" التشابك؟ هذا الأمر يقودنا لمفهومٍ آخر، وهو أن كل وصلة بين عصبونين تمتلك قيمة عددية تعرف باسم الوزن (Weight). بالنسبة لطبقة الدخل، قيمة تفعيل العصبونات هي قيمة البيكسل الموافق في صورة الدخل، وعلى اعتبار التعامل مع صورة رمادية، فهذا يعني أن قيمة تفعيل أي عصبون في طبقة الدخل قد تكون أي قيمة ما بين الصفر (التي تمثل بيكسل اللون الأسود) و255 (أي قيمة بيكسل اللون الأبيض).
الآن نريد الانتقال إلى الطبقة المخفية الأولى، ومن أجل حساب قيمة تفعيل العصبون الأول فيها، يجب أن نقوم بضرب قيمة تفعيل كل عصبون من طبقة الدخل بوزن وصلته مع العصبون الأول من الطبقة المخفية، ومن ثم يتم جمعها مع بعضها البعض، ثم تُكرَّر هذه العملية من أجل كافة عصبونات الطبقة المخفية الأولى. بعد حساب قيم تفعيل عصبونات الطبقة المخفية الأولى يتم الانتقال للطبقة المخفية الثانية بنفس الطريقة، وهكذا حتى الوصول لطبقة الخرج. يعني الكلام السابق أن تفعيل عصبونات الطبقة الأولى يتم بحسب قيم البيكسلات في الصورة المدخلة، وبما أن قيم البيكسلات ستختلف بحسب الرقم المكتوب، فإن هذا الأمر يعني أن عصبونات الطبقة المخفية الأولى سيتم تفعيلها بآليةٍ تؤدي إلى اكتشاف -والتعرف على- أنماط دقيقة معينة (خطوط ومنحنيات قصيرة)، وهذه الأنماط بدورها ستؤدي إلى تفعيل عصبونات الطبقة المخفية الثانية بقيمٍ تساهم في التعرف على أنماطٍ رئيسية (دوائر، أقواس، خطوط مستقيمة) تم استنتاجها من الأنماط الدقيقة المكتشفة في الطبقة التي سبقتها، وهذا الأمر سيؤدي إلى تفعيل عصبونات الخرج لتعطي القرار النهائي الذي يشير إلى أرجحية أن تكون الأنماط المكتشفة تمثل رقماً دون الآخر.
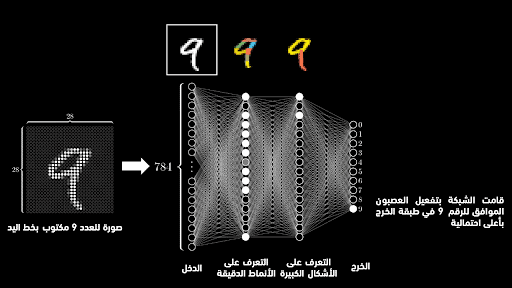
مصدر الصورة: قناة 3Blue1Brown | تعديل وتعريب: إم آي تي تكنولوجي ريفيو العربية
التعلم : كيف يتم تحديد قيم أوزان الوصلات؟
تطرح الشرح السابق لكيفية قيام الشبكة بتنفيذ خطوات المعالجة الخاصة بها، ولكن هناك سؤال هام: طالما تلعب أوزان الوصلات بين العصبونات دوراً هاماً في العمليات الحسابية الخاصة بحساب قيم تفعيل عصبونات الطبقة التالية، لكن كيف يتم تحديد قيم هذه الأوزان؟ هذا ما يقود إلى مفهوم التعلم.
عندما تبدأ الشبكة بالعمل للمرة الأولى فإنها ستمتلك قيماً أولية لأوزان الوصلات (وكذلك بعض البارامترات الأخرى، ولكن سنجعل الشرح هنا مقتصراً على الأوزان للتبسيط)، ومن ثم يتم تمرير صور لأرقامٍ مكتوبة بخط اليد. في البداية، ونظراً لكون قيم الأوزان غير مضبوطة بشكلٍ دقيق، لن تكون النتائج التي ستقدمها الشبكة صحيحة؛ حيث لن تستطيع في البداية اكتشاف الأرقام المكتوبة على نحوٍ جيد.
لحسن الحظ، يمكن تزويد الشبكة بآلية تخبرها إن كانت تعمل بشكلٍ صحيح أم لا، وكذلك مدى دقة القرارات التي تخلص إليها. هذا الأمر يتم عبر حساب نسبة التعرف الصحيح التي تقوم به الشبكة مع كل مرة يتم إدخال صورة إليها، وتزويد هذه المعلومات للشبكة لتقوم بتعديل قيم أوزان الوصلات بين العصبونات. مع تكرار عمليات إدخال الصور التي ستؤدي إلى تعديل قيم أوزان وصلات العصبونات، ستستطيع الشبكة معرفة الأوزان التي تؤدي لأعلى احتمالية تعرّف صحيح وتلك التي تؤدي لاحتمالية تعرّف خاطئ. هذا الأمر يقود لاستنتاج هام: الشبكات العصبونية تمتلك شهية عالية جداً للبيانات! بمعنى أنه كلما ازدادت كمية بيانات التدريب تحسنت دقة عمل الشبكة.
هذا الإجراء السابق هو ما يعرف باسم: التعليم (Learning)، والطريقة الموصوفة سابقاً هي ما تعرف باسم: التعلم الموجه (Supervised Learning) أو التعليم الخاضع للإشراف؛ وذلك لأن المبرمج هو من يقوم بإخبار الشبكة العصبونية إن كان عملها صحيحاً أو خاطئاً، وكذلك كيفية تحسين دقة عملها ونتائجها. وهنالك نمط آخر من التعليم لا يتدخل فيه المبرمج ولا يوجد عبره طريقة لإخبار الشبكة عن صحة نتائجها، بل تترك وحدها لتستنتج القرارات المتعلقة بالخرج بناءً على البيانات المدخلة إليها أثناء مرحلة التدريب، وهذا النمط من التعليم يعرف باسم: التعلم غير الموجه (Unsupervised Learning)، أو التعلم غير الخاضع للإشراف.
ومن المهم ذكره هنا في هذا السياق أن المثال السابق (التعرف على الأرقام المكتوبة بخط اليد) هو المثال الأولي والكلاسيكي لشرح مفاهيم الشبكات العصبونية. لكن التطبيقات الفعلية للشبكات العصبونية أعقد من ذلك، وبعضها وصل إلى درجاتٍ بالغة التعقيد وإلى قدراتٍ متقدمة جداً، مثل الشبكة العصبونية الخاصة بجوجل "ألفا جو"، التي تمكنت من تعلم لعبة جو الشهيرة والتفوق على كل منافسيها البشر. أخيراً، فإنه من المهم أيضاً معرفة أن للشبكات العصبونية أنماطاً متنوعة، لكل منها ميزات تجعلها مفضلة في تطبيقاتٍ معينة، مثل تفضيل استخدام الشبكات العصبونية الملتفة (Convolutional Neural Networks) في مجال معالجة الصور.
أنواع الشبكات العصبونية الاصطناعية
هناك عدة أنواع للشبكات العصبونية الاصطناعية، إليكم شرح بسيط لأهمها:
-
الشبكات العصبونية أمامية التغذية:
تُعد الشبكات العصبونية أمامية التغذية أول وأبسط أشكال الشبكات العصبونية؛ حيث تتم معالجة البيانات فيها باتجاه واحد فقط. وتتألف هذه الشبكة من طبقة دخل وطبقة خفية وطبقة خرج، وعلى الرغم من إمكانية مرور البيانات عبر عدة عقد مخفية، إلا أن حركتها تكون بالاتجاه الأمامي حصراً من طبقة الدخل إلى طبقة الخرج.
-
الشبكات العصبونية الالتفافية:
هي نوع من أنواع الشبكات العصبونية الاصطناعية المُصممة لتعمل بطريقة تحاكي النظام البصري لدى الإنسان. تتألف الشبكات العصبونية الالتفافية من طبقات متعددة يكون خرج كل منها عبارة عن دخل للطبقة التالية. وتتمثل وظيفة الطبقة الأولى عادةً بتحديد الميزات الأولية في الصور مثل الحواف الأفقية والعمودية والقطرية. ثم تقوم الطبقة التالية بتحديد الميزات الأعقد مثل الزوايا أو الأشكال الناتجة عن تجميع الحواف. ومع التقدم من طبقة إلى أخرى تبدأ عملية تحديد الميزات عالية المستوى مثل الأشياء والوجوه وغيرها. وتستخدم بشكل أساسي في تطبيقات التعلم العميق التي تهدف إلى تصنيف الصور أو تجميع الصور المتشابهة أو التعرف على الأشياء في الصور ومقاطع الفيديو، مثل التعرف على الوجوه أو الأشخاص أو الأورام في الصور الطبية وغيرها. تتميز الشبكات العصبونية الالتفافية بقدرتها على تحديد أهمية الأشياء والعناصر الموجودة ضمن الصور والتمييز بينها. وتتطلب قدراً أقل من المعالجة المُسبقة لصور الدخل مقارنة بغيرها، وذلك نظراً لكونها قادرة على تعلم استخلاص الميزات تلقائياً عند تدريبها بشكل كافي.
-
الشبكات العصبونية المتكررة:
تعتمد هذه الشبكات على البيانات التسلسلية، وتستخدم في تطبيقات التعلم العميق التي تتعامل مع البيانات المتتابعة والسلاسل الزمنية مثل ترجمة اللغات ومعالجة اللغة الطبيعية والتعرف التلقائي على الكلام المنطوق. ومن أهم الأمثلة على استخدامها المساعدات الصوتية مثل سيري وأليكسا والبحث الصوتي وخدمة الترجمة من جوجل. تعتبر الشبكات العصبونية المتكررة قديمة نسبياً، حيث ظهرت لأول مرة في ثمانينيات القرن الماضي. لكن لم تتم الاستفادة من إمكانياتها بالشكل الأمثل إلا في السنوات الأخيرة تزامناً مع توفر البيانات الضخمة والقدرات الحاسوبية العالية. وتتمتع هذه الشبكات بميزة "الذاكرة" التي تسمح لها بأخذ معلومات من بيانات الدخل السابقة للتأثير على بيانات الدخل والمخرجات الحالية. فعلى عكس الشبكات العصبونية العميقة الأخرى التي تفترض أن المدخلات مستقلة عن المخرجات، يعتمد الخرج في الشبكات المتكررة على العناصر السابقة في تسلسل البيانات.
ما هو عدد نقاط البيانات اللازم في تدريب الشبكات العصبونية الاصطناعية؟
هذا سؤال تصعب الإجابة عليه؛ هل لديك البيانات الكافية لتدريب الشبكة العصبونية؟ تكمن أهمية الإجابة في أن حجم بيانات التدريب يلعب دوراً حاسماً في تطوير نموذج ذكاء اصطناعي ناجح؛ فإذا كان حجم البيانات غير مناسب سيؤدي ذلك إلى ضعف دقة النموذج وربما إلى مشاكل مثل فرط الملاءمة أو نقصها.
هناك العديد من العوامل التي تلعب دوراً في تحديد الحجم الأمثل لبيانات التدريب. على سبيل المثال لا الحصر، إذا كنت ترغب في بناء شبكة عصبونية لفرز صور لصنفين فقط مثلاً القطط والكلاب، لن تحتاج إلى العدد الكبير من البيانات الذي يجب عليك استخدامه فيما لوكنت ترغب في تصنيف 50 نوعاً من الحيوانات. عامل آخر يتمثل في توفر قيم ابتدائية جيدة للأوزان في شبكتك العصبونية. علاوة على ذلك، قد لا تمتلك حرية القرار فيما يتعلق بشأن حجم البيانات التي ستدرب عليها الشبكة العصبونية، فقد تكون البيانات بين يديك هي كل ما هو متوفر، في هذه الحالة قد تلجأ إلى حل آخر مثل البيانات المصطنعة لزيادة حجم البيانات.
مع أخذ كل ما سبق بعين الاعتبار، يذكر البروفسور المصري ياسر أبو مصطفى، المختص في علوم الحاسوب بمعهد كاليفورنيا للتكنولوجيا، قاعدة بسيطة وهي أن حجم بيانات التدريب يجب أن يكون 10 أضعاف درجة حرية النموذج، أي لو كان لديك شبكة عصبونية تحتوي 3 أوزان فإنك تحتاج إلى 30 نقطة من البيانات لتدريبها عليها.