نسمع كل يومٍ عن الكثير من التقنيات المستقبلية التي من شأنها تغيير شكل حياتنا بشكلٍ جذريّ؛ فهنالك الذكاء الاصطناعيّ الذي دخل مجالاتٍ متنوعة ومتعددة وهنالك التقانة النانوية التي تتيح التلاعب بالمادة عند أبعادٍ متناهية الصغر تصل إلى حدود الذرة الواحدة، وهنالك أمورٌ سبق وأن كانت من سرديات الخيال العلميّ وأصبحت واقعاً نعيشه ونألفه مثل الواقع الافتراضيّ والواقع المعزز.
وهنالك أيضاً أمرٌ آخر، هو: الحواسيب الكمومية، التي يمكن القول بأنها من أشد التقنيات غرابةً وأكثرها إثارةً بسبب اعتمادها على مبادئ ومفاهيم من الصعب لنا فهمها في عالمنا المرئيّ، ولكنها تمثل القوانين التي تحكم عالم الذرات والجسيمات دون الذرية. مثل أي تقنيةٍ واعدة أخرى، يكثر الحديث حول القدرات التي قد تتيحها الحواسيب الكمومية عندما تصل لمرحلة التفوق الكمومي Quantum Supremacy، أي عندما تصبح قادرة على إنجاز العمليات الحسابية بكفاءةٍ أعلى بكثير من الحواسيب التقليدية اعتماداً على مبادئ ومفاهيم فيزياء الكم.
وفي حين أن هناك حماساً وترقباً كبيرين من قِبل المجتمع العلميّ والتقنيّ للحواسيب الكمومية، فإن هذا الحماس محفوفٌ بالحذر من قِبل البعض؛ فرغم كونه يتيح للحواسيب الكمومية تفوقاً كبيراً في سرعة إنجاز العمليات الحسابية، مما قد يسهم في إيجاد حلولٍ للعديد من المشاكل المستعصية، إلا أن هذه القدرة -أي الإنجاز فائق السرعة للعمليات الحسابية- قد تمثل خطراً على جانبٍ هام نعتمد عليه في حياتنا بشكلٍ كبير، وهو: الاتصال الآمن والموثوق بالخدمات على الإنترنت عبر معايير التشفير والحماية. فكيف يمكن للحواسيب الكمومية أن تشكل خطراً على مجال الحماية والخصوصية؟
حول الحواسيب الكمومية
تعتمد الحواسيب التقليدية التي نستخدمها اليوم على مبدأ بسيط لتمثيل البيانات، وهو: البتات الرقمية، وهي ببساطة عبارة عن سلاسل من الأصفار والواحدات. كل ما نقوم باستخدامه وكل ما نتفاعل معه ينتهي به المطاف على مستوى المعالج ليصبح سلسلةً من الأصفار والواحدات، سواء كان ذلك في الفيديوهات والصور التي نتشاركها عبر وسائل التواصل الاجتماعيّ أو حتى الملفات النصية أو الملفات بصيغة بي دي إف (PDF) أو حتى البرامج نفسها التي نستخدمها ونعتمد عليها، جميعها يتم "ترجمتها" وتحويلها من الشكل الذي نراه أمامنا لتصبح أصفاراً وواحدات مرتبة بطريقةٍ معينة ليكون المعالج قادراً على فهمها وإجراء العمليات المختلفة عليها.
ولكن على الصعيد الفيزيائي، ما هي هذه الأصفار والواحدات؟ إنها ببساطة قيم كهربائية: يمثل الواحد حالة مرور تيار كهربائيّ بينما يمثل الصفر حالة عدم مرور تيار كهربائيّ (الأمر أعقد من ذلك بقليل، ولكن لنتفق على تمثيله بهذه الطريقة)، ولهذا السبب يتم استخدام الترانزيستورات كوحدات بناء أساسية للمعالجات لأنه يمكن التحكم في عملها كمفتاح؛ عندما يكون الترانزيستور في حالة عمل فإنه سيمرر التيار الكهربائيّ وسنفهم ذلك على أنه بت ذو قيمة واحد، بينما يؤدي إغلاق الترانزيستور لعدم مرور تيار وسنفهم ذلك على أنه بت ذو قيمة صفر. وعبر التبديل السريع جداً للترانزيستورات بين هاتين الحالتين (فتح وإغلاق) وعبر تضمين المعالج بعددٍ كبيرٍ جداً من الترانزيستورات (يصل حتى عدة مليارات في المعالجات الحالية) سيكون بالإمكان معالجة المعلومات المختلفة التي نراها.
بحالة الحواسيب الكمومية، فإن عملية تمثيل البيانات تعتمد على مفهومٍ آخر: البت الكمومي أو كما يعرف اختصاراً باسم: الكيوبت (Qubit)، حيث يمكن للكيوبت الواحد أن يكون صفراً، أو واحداً أو في حالة تراكب (Superposition): بمعنى أن يكون صفراً وواحداً في نفس الوقت. بذلك، وإذا سألنا: ما هي قيمة الكيوبت الآن؟ فإن الجواب سيكون احتمالاً، وليس قيمةً مطلقة كما هو الحال في الحواسيب التقليدية، ومن دون إجراء قياس لن تكون هنالك إمكانية لمعرفة قيمة -أو لنقل حالة- الكيوبت. وعندما نجري قياساً فسيختفي الغموض وستزول الخواص الاحتمالية، وسيمتلك الكيوبت إحدى قيمتين: الصفر أو الواحد.
ترجع هذه الخاصية لميكانيك الكم والاعتماد على قوانينه في توصيف سلوك الجسيمات دون الذرية، التي يمكن لها أن تتواجد في حالة تراكب، ولن يكون بالإمكان معرفة حالة الجسيم (أو إحدى خواصه) إلا عبر إجراء قياسٍ لها، وعندها سينهار التابع الموجي الذي يصف الجسيم وستنتهي حالته لقيمةٍ محددة. تم التعبير عن هذا الأمر عبر تجربةٍ ذهنيةٍ شهيرة منسوبة لعالم الفيزياء النمساوي إرفين شرودينجر، والمعروفة باسم: قطة شرودينجر (Schrödinger's cat)، والتي تقول: إذا وضعنا قطة في علبة مغلقة مع سمٍّ يتم تفعليه عبر تفكك مادةٍ مشعة، فكيف سنعلم إن كانت ميتة أو حية؟ طالما أننا لن نفتح العلبة فإن القطة قد تكون حية وميتة بنفس الوقت، وذلك لأن احتمال حصول تفكك للمادة المشعة -وبالتالي تفعيل السم- مساوٍ لاحتمال عدم تفكك المادة المشعة. معرفة حالة القطة يتطلب إذن فتح العلبة، وعندها لن تكون القطة حية وميتة بنفس الوقت، بل إما حية وإما ميتة. بشكلٍ مشابهٍ لهذا الأمر، فإن حالة الكيوبت الكمومي قد يكون صفر وواحد بنفس الوقت إلى أن نجري قياساً ونتيقن من حالته.
بهذه الصورة، وبما أن الكيوبت يمكن أن يمتلك قيماً أكثر من البت الرقمي التقليدي، فهذا يعني أنه سيكون بإمكانه تمثيل كمية أكبر بكثير من المعلومات، على الأقل من الناحية النظرية. وحتى هذه اللحظة، لا يوجد شيءٌ مريب في الأمر ولا يوجد داعٍ للقلق من الحواسيب الكمومية، أليس كذلك؟ علينا تذكر أمر هام: عملية تحديد قيمة الكيوبت (أي إجراء قياس بمصطلحات فيزياء الكم) تتطلب حساب الاحتمالات الممكنة المختلفة التي يمكن له أن يمتلكها، وذلك قبل أن نقول عنه إنه ذو قيمة صفر أو واحد بشكلٍ أكيد. التعامل مع احتمالاتٍ أكبر يعني التعامل مع كمية بيانات أكبر، ويعني معالجة معلومات أكثر، وذلك قبل أن نعرف قيمة الكيوبت نفسه. هذه العمليات نفسها غير موجودة في الحواسيب التقليدية، مما يجعل البت الرقمي التقليدي يمثل كمية معلومات أقل بكثير من الكيوبت الكمي.
هذه النقطة -أي القدرة على تمثيل ومعالجة كمية كبيرة من المعلومات عبر كيوبت واحد- هي التي تمثل تفرد وتخصص الحواسيب الكمومية، ولكنها بنفس الوقت تمثل مصدر القلق منها؛ لأن معايير الحماية والتشفير قائمة على جعل العمليات الرياضية المطلوبة لكسر رموز التشفير طويلة ومعقدة وتتطلب وقتاً زمنياً طويلاً.
معيار التشفير والحماية RSA
في عالم الاتصالات الرقمية، يتم استخدام معايير تضمن إنشاء قناة اتصال موثوقة وتجعل من مهمة اختراق المعلومات صعبة قدر الإمكان، ويعتبر معيار RSA من أشهر هذه المعايير، وهو قائم على فكرة تبادل المفاتيح بين طرفي الاتصال، وهذه المفاتيح ما هي فعلياً إلا سلسلة طويلة من الأرقام. هنالك نوعان من المفاتيح: المفتاح العام Public Key والمفتاح الخاص Private Key. المفتاح العام يمثل الرسالة بعد أن يتم تشفيرها، وكي يكون المستقبِل قادراً على فهمها، فإنه سيحتاج إلى مفتاحٍ خاص يخبره بكيفية فك تشفير هذه الرسالة وفهم محتواها.
من أجل توليد المفتاح العام، يتم الاعتماد على مبدأ في الرياضيات يعرف بالتوابع أحادية الجهة One-Way Functions، التي تمثل طريقةً سهلة لإنشاء قيمة عددية ما، وبنفس الوقت سيكون من الصعب إجراء العملية المعاكسة؛ أي أننا إذا عرفنا المفتاح العام، فسيكون من الصعب معرفة كيفية تشكيله. بهذا السياق يتم استخدام الأعداد الأولية، ويتم تشكيل المفتاح العام عبر ضرب عددين أوليين كبيرين جداً ببعضهما البعض، لينتج عنهما عددٌ آخر كبير جداً. وهكذا ومن أجل معرفة محتوى الرسالة الأصلية يجب أن نكون قادرين على تحويلها من شكلها المشفر باستخدام المفتاح العام لشكلها الأصليّ، وهذا يتطلب معرفة العوامل العددية التي تم ضربها ببعضها البعض لتشكيل المفتاح العام.
في علم الرياضيات، يمكن النظر لأي عدد على أنه حاصل ضرب عددين آخرين، وهي العملية المعروفة باستخدام تحليل الأعداد Factorization، التي تؤدي للتوصل إلى كل العوامل العددية التي يمكن ضربها ببعضها لتشكيل رقمٍ ما. لو أخذنا عدداً مثل 40، فإنه قد ينتج عن ضرب 10 مع 4، أو ضرب 20 مع 2، أو ضرب 8 مع 5. لو اعتبرنا الآن أن الرسالة الأصلية هي الرقم 5، فإن المفتاح العام هو 40، وبالتالي فإن المفتاح الخاص هو 8. من أجل معرفة الرسالة الأصلية (أي العدد 5) يجب معرفة المفتاح الخاص (أي العدد 8)، لأن تقسيم 40 على 10 سيعطينا العدد 4، وهو ما لا يمثل الرسالة المطلوبة. وفي عالم التشفير، لا يتم استخدام مفاتيح عامة من خانتين (مثل العدد 40)، بل مفاتيح عامة مكونة من سلسلة عددية من مئات الأرقام التي تنتج عن ضرب عددين أوليين كبيرين جداً.
بالرّغم من قوة الحواسيب وتطورها، فإن عملية تحليل العدد الذي يمثله المفتاح العام ستتطلب وقتاً طويلاً جداً، مما يجعل عملية اختراق المعيار وفك تشفير الرسالة أمراً مستحيلاً من الناحية العملية، وبالوقت الحاليّ، تعتمد معايير RSA على مفاتيح بتمثيلٍ ذي قيمةٍ تتراوح بين 1024 وحتى 4096 بت، وحتى عام 2019، تم إثبات أنه يمكن اختراق المفاتيح التي تمتلك تمثيلاً قدره 795 بت (أي تحليلها رياضياً من أجل التوصل للرقم الذي يمثل المفتاح الخاص، وبالتالي معرفة محتوى الرسالة). بالنسبة للمفاتيح التي تمتلك تمثيلاً قدره 1024 بت، فإنه لم تعد تُعتبر آمنة كما كانت من قبل، وفي الوقت الحاليّ، فإن استخدام معيار RSA لتوليد مفتاح بتمثيلٍ قدره 2048 بت (أي سلسلة من الأعداد طولها 617 عدداً صحيحاً) يعتبر أمراً آمناً، ومن شبه المستحيل للقدرات الحاسوبية التقليدية أن تتمكن من اختراق الرسائل المشفرة باستخدام هذا المعيار، وبشيءٍ من الدقة: تشير التقديرات الحالية إلى أن فك تشفير رسالة ذات مفتاح بتمثيل 2048 بت قد تتطلب حوالي 300 ترليون سنة. [توضيح: عند القول بأن تمثيل المفتاح هو 1024 بت -كمثال- فهذا الرقم ليس هو العدد الصحيح الذي يمثله المفتاح، بل عدد البتات الرقمية المطلوبة لتمثيل العدد بالنسبة للحاسوب].
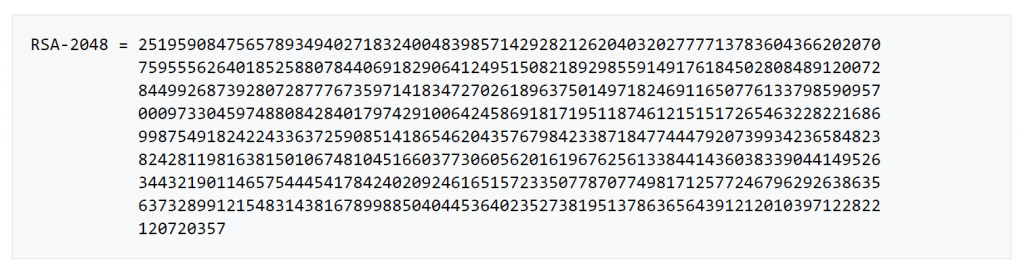
مصدر الصورة: ويكيبيديا
خوارزمية شور : معادلة تنتظر الحاسوب الكمومي
سنة 1994، قام عالم الرياضيات في جامعة إم آي تي بيتر شور (Peter Shor) بنشر معادلةٍ رياضية توضح أنه يمكن فك تشفير الرسائل المرمزة باستخدام معيار RSA ببساطة وبسهولة شديدة، وفي زمنٍ قصيرٍ جداً، ولكن ذلك يتطلب أمراً واحداً: امتلاك حاسوبٍ كموميّ ذي عدد هائلٍ جداً من البتات الكمومية.
تتلخص فكرة خوارزمية شور بمبدأ بسيط: إذا كان لدينا عددٌ ضخمٌ يدعى N، فإن المطلوب هو تحديد عوامله الأولية. عمد بيتر شور في تصميم خوارزميته على استغلال الخواص الاحتمالية (اللاحتمية) التي تتصف بها البتات الكمومية، ولذلك فإن معادلته احتمالية تقوم بإعطاء الناتج باحتمال نجاح مرتفع، كما أن انخفاض احتمالية الفشل يتناسب طرداً مع زيادة عدد مرات تكرار الخوارزمية. وهكذا، أظهرت الخوارزمية قدراتٍ متقدمة في قدرتها على معرفة العوامل الأولية التي تشكل المفتاح العام في معيار RSA، نظرياً، ولكن تطبيقها العمليّ يستوجب حاسوباً كمومياً. ويمكن فهم أهمية خوارزمية شور بشكلٍ أكثر بساطة إذا علمت أنها ساهمت -عبر استغلالها واستثمارها لبنية الحواسيب الكمومية- في تقليص الزمن اللازم لإجراء عملية اكتشاف المفتاح الخاص (أي تحليل العوامل الرياضية للمفتاح العام) بشكلٍ أسيّ.
ولسوء حظ بيتر شور، ولحسن حظ معايير الحماية، فإن الحاسوب الكموميّ اللازم استخدامه لكسر معيار الحماية RSA-2048 ضخمٌ جداً، حيث أشارت تقديراتٌ سابقة أنه يجب أن يمتلك حوالي 4 مليار بت كمومي، وأشارت أفضل التقديرات من جوجل أنه يمكن إنجاز ذلك باستخدام 20 مليون بت كمومي. أين نحن من ذلك؟ أفضل الحواسيب الكمومية المتوافرة حالياً هو حاسوب جوجل الكمومي الذي يمتلك 72 كيوبت، وبالتالي فإن امتلاك حاسوبٍ كموميّ قادر على تنفيذ خوارزمية شور لكسر معيار RSA-2048 لا يزال أمراً بعيداً جداً.
وبالنسبة لتنفيذ الخوارزمية نفسها، فإن التطبيق الأول لها ضمن حاسوبٍ كموميّ حدث سنة 2001، عندما قامت شركة آي بي إم بإجراء تحليلٍ لعوامل العدد الأولي 15، واستخلاص عوامله (3 و 5) باستخدام خوارزمية شور ضمن حاسوبٍ كموميّ يتكون من 7 بتات كمومية، وفي سنة 2012، تم إجراء تحليل لعوامل العدد 21. وبالمقارنة، السلسلة العددية الممثلة للمفتاح العام في معيار RSA-2048 طولها 617 عدد.
هل الأمن الرقمي في خطر بسبب الحواسيب الكمومية؟
ذكرنا أن كسر معيار RSA تم أول مرة سنة 1999، وذلك بالنسبة للمفاتيح التي تمتلك تمثيلاً قدره 512 بت، ولكن ما لم نذكره أن هذه العملية تطلبت زمناً قدره 6 أشهر من أجل فك تشفير الرسالة، وعندما تم كسر معيار RSA ذي تمثيل 768 بت سنة 2009، استغرقت العملية جهداً قدره 4 سنوات متواصلة من عمل ألمع علماء الرياضيات والأعداد. ولذلك، فإن الحديث عن "اختراق" خوارزمية تشفير معينة لا يعني إنجاز ذلك بلمح البصر، بل إثبات إمكانية فك تشفير الرسائل المرمزة باستخدام الخوارزمية المعنية، بغض النظر عن الزمن اللازم لإتمام هذه العملية، فضلاً عن أننا نتحدث عن امتلاك العلماء القائمين على هذه الأعمال لقدراتٍ حاسوبية متقدمة فضلاً عن كونهم من المتخصصين في مجال عملهم.
من ناحيةٍ أخرى، وفيما يتعلق بالحواسيب الكمومية، فإن ما يجب معرفته هو أننا ما زلنا بعيدين في الوقت الراهن عن امتلاك حاسوبٍ كموميّ متفوق قادر على تطبيق المفاهيم والمبادئ النظرية التي تتيح له اختصار الوقت اللازم لإنجاز عمليات المعالجة مقارنةً مع الحاسوب التقليديّ. هناك مشاكل كثيرة ترتبط بالحواسيب الكمومية، مثل الحساسية الحالية تجاه الضجيج، وضرورة تشغيل داراتها عند شروطٍ صعبة (مثل استخدام نواقل فائقة عند درجة حرارة قريبة من الصفر المطلق أي حوالي -273 درجة مئوية)، فضلاً عن صعوبة تأمين استقرار حالة البتات الكمومية. ويعتقد البعض أننا قد لا نحصل أبداً على حاسوبٍ كموميّ بالشكل الذي نتصوره. وفي كل الأحوال، فإنه من المؤكد أن حصولنا على القدرات الحاسوبية الكمومية "الخارقة" هو أمرٌ سيتطلب عقوداً طويلة من البحث والتطوير.
لكن على فرض أن إنجاز الحاسوب الكموميّ الذي يمتلك 4 مليار بت كمومي اللازمة لكسر معيار RSA-2048 وفك تشفير كل الرسائل، فإننا نستطيع أن نكون مرتاحي البال -نوعاً ما- بسبب العمل الذي يجري في الوقت الحالي، والهادف إلى تطوير معايير تشفير كمومية تعمل على الحواسيب الكمومية، والتي يتم وصفها من قِبل البعض على أنها مستحيلة الاختراق، حتى باستخدام أعتى الحواسيب الكمومية.
والسؤال: هل تشكل الحواسيب الكمومية خطراً على الأمن الرقمي؟ نعم نظرياً، وعملياً فإن الأمر مستبعد، على الأقل في المستقبل قريب الأمد.

