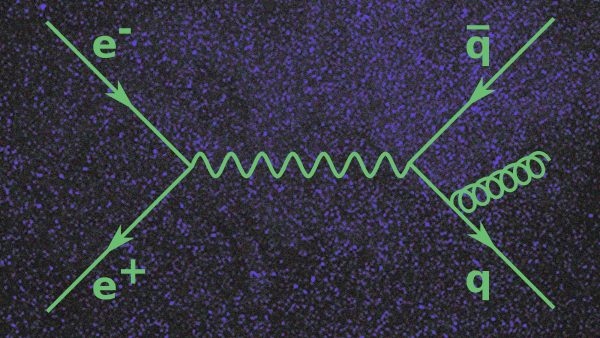
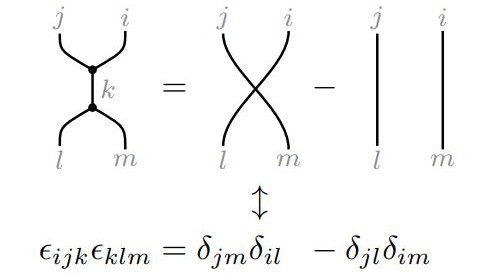في العام 1948، نشرت مجلة Physical Review بحثاً بعنوان مقاربة زمكانية للديناميكيات الكهربائية الكمومية لفيزيائي شاب اسمه ر. ب. فاينمان من جامعة كورنيل. وصف البحث طريقة جديدة لحل المسائل في الديناميكيات الكهربائية باستخدام المصفوفات، غير أن هذا البحث يُذكر حتى الآن بفضل اختراع أكثر تأثيراً، هو: مخطط فاينمان، الذي ظهر مطبوعاً في هذا البحث للمرة الأولى.
أحدثت مخططات فاينمان أثراً كبيراً في الفيزياء، وهي عبارة عن تمثيلات مرئية للعلاقات الرياضية التي تصف التفاعلات بين الجسيمات تحت الذرية. فمن الناحية الرياضية، يُمثل كل تفاعل بمتسلسلة لا نهائية، ما يعني صعوبة هائلة في التعبير الكتابي عن هذه التفاعلات بين الجسيمات، بما فيها التفاعلات الأكثر بساطة.
تمثلت عبقرية فاينمان بتمثيل هذه السلاسل برسومات على شكل خطوط بسيطة، بحيث تتيح للعلماء التفكيرَ في فيزياء الجسيمات بأساليب جديدة وثورية.
بدأ فاينمان وغيره على الفور بتعزيز أفكارهم باستخدام هذا الاختزال المرئي. وبالفعل، فقد كتب الفيزيائي الأميركي فرانك ويلشيك -الذي عمل مع فاينمان في الثمانينيات- قائلاً: "لولا مخططات فاينمان، لكان من المستحيل -ومن دون مبالغة- أن أجري الحسابات التي أدت إلى فوزي بجائزة نوبل عام 2004".
بطبيعة الحال، تعتمد الكثير من المجالات الفيزيائية الأخرى أيضاً على نماذج رياضية معقدة، وهو ما يثير تساؤلاً مشروعاً حول إمكانية تبسيط هذه الحسابات باستخدام مخططات مبتكرة، وربما إطلاق حقبة جديدة من الإبداع في الفيزياء، تماماً كما فعل فاينمان.
وهنا يأتي دور جون هوي كيم في جامعة سيئول الوطنية في كوريا الجنوبية وبعض من زملائه، الذين توصلوا إلى ابتكار مشابه يُستخدم للتفاضل الشعاعي؛ أي أنه اختزال رسومي لواحدة من أكثر الأدوات الرياضية استخداماً وتأثيراً في العلم. يقول الباحثون: "نتوقع أن يؤدي التفاضل الشعاعي الرسومي إلى زيادة سهولة تعلم واستخدام التفاضل الشعاعي، كما فعلت مخططات فاينمان في نظرية الحقل الكمومي".
ولكن لنعد إلى بعض المعلومات الأساسية أولاً؛ حيث يُعرف التفاضل الشعاعي بأنه فرع من الرياضيات يدرس التفاضل والتكامل للحقول الشعاعية. وتنبع أهميته في الفيزياء من أن كل شيء في الكون تقريباً يمكن تمثيله على شكل حقول شعاعية، من الحقول الكهرطيسية والثقالية وصولاً إلى تدفق الموائع، وغير ذلك.
ولهذا السبب، يجب على كل طالب جامعي يدرس الفيزياء أو الهندسة أن يمضي ساعات عديدة من السعادة الغامرة وهو يصارع العلاقات الرياضية والرموز الغريبة المستخدمة للتعبير عنها. وتكمن المشكلة في أن الحقول الشعاعية كيانات معقدة؛ حيث إنها تنسب شعاعاً واحداً إلى كل نقطة من الفضاء ثلاثي الأبعاد، ويمكن أن تُمثل نفسها ببنى رياضية أكثر تعقيداً تسمى المتشعبات القابلة للمفاضلة. أي أن الحقل الشعاعي -بأبسط أشكاله- يمكن أن يكون عبارة عن مجموعة لانهائية من الأشعة.
يمثل الرياضيون هذه الحقول باستخدام طريقة ترميز الدليل؛ حيث يمكن أن يُكتب الشعاع على شكل ai حيث i يساوي 1 أو 2 أو 3، ويمكن أن يُكتب أيضاً بهذه الطريقة: [a1, a2, a3].
تظهر المشاكل عندما تتفاعل هذه المقادير مع بعضها البعض رياضياً. يمكن جداء الحقول الشعاعية بمقادير سلمية أو ببعضها البعض بطريقتين، تُعرفان باسم جداء النقطة وجداء التقاطع. ويمكن أن تكون النتائج شديدة التعقيد على شكل مصفوفات ضخمة متعددة الأبعاد.
في جميع هذه الحالات، يجب تتبع أدلة الحقول الشعاعية بحرص، ويعرف جميع الفيزيائيين سهولة ارتكاب خطأ في الأدلة، والعمل المضني المطلوب لاكتشاف هذا الخطأ. علاوة على ذلك، هناك أيضاً مسألة دراسة تغير هذه الحقول مع الزمن، أو مع متحول آخر، وهي ما تسمى بمسألة التفاضل، التي طوّر الفيزيائيون عدة أدوات للتعامل معها باسم المؤثرات، وقد يكون أشهرها مؤثر دل أو نابلا.
يُلخَّص إنجاز كيم وزملائه بتطوير ترميز رسومي يحل محل ترميز الدليل؛ حيث يُمثل الشعاع بصندوق يتصل به خط، أما المقدار السلمي فلا توجد خطوط ممتدة منه.
عند إجراء جداء نقطة بين شعاعين، تكون النتيجة مقداراً سلمياً، وفي ترميز كيم وزملائه لجداء النقطة، تتصل الخطوط الخارجة من الأشعة مع بعضها البعض، وينتج عن ذلك عنصر جديد لا تمتد منه أية خطوط، أي أنه مقدار سلمي.
غير أن جداء التقاطع بين شعاعين يؤدي إلى شعاع آخر، ويتعامل الترميز الجديد مع هذه الحالة أيضاً؛ حيث إن الترميز الرسومي لشعاع النقطة يأخذ شكل حرف Y، إذ تتصل الخطوط الخارجة من كل من الشعاعين بخط ثالث يمتد إلى الخارج، أي أنها تشكل شعاعاً.
هذه مجرد أساسيات، حيث يتضمن الترميز الجديد مجموعة كبيرة من الأدوات الرياضية الأخرى، مثل معامل دل والعديد من المتطابقات الهامة المستخدمة في التفاضل الشعاعي. كما أن هذه الأفكار تمتد إلى التنسورات أو الموتّرات، وهي عناصر رياضية أكثر تعقيداً، يحتوي كل منها على دليلين أو أكثر.
وتبين النتائج سهولة كبيرة في العمل؛ فقد أثبت كيم وزملاؤه أن ترميزهم يحول التعابير الرياضية المعقدة إلى رسومات بسيطة نسبياً، تماماً مثل مخططات فاينمان، ويقولون: "تتسم هذه اللغة الجديدة بطابع منطقي سهل الاستخدام، وتقوم بشكل ذاتي بتبسيط تعابير الموترات".
يمثل هذا الترميز أداة هامة، ويقول الباحثون إن طريقتهم تحول تفاضل الحقول الشعاعية إلى مهمة بصرية، بدلاً من شكلها الحالي الذي يُعتبر أقرب إلى البناء بقطع تركيبية، كما يقولون: "إن إجراء التجارب المسلية برسم هذه المخططات الراقصة سيكون أقرب إلى حالة طفل يلعب بألعاب تعليمية مثل قطع الليجو أو الكتل المغناطيسية. وكما تُعتبر مخططات فاينمان هي اللغة الأكثر طبيعية لتوصيف العمليات فائقة الصغر للجسيمات الأولية، فإن الترميز الرسومي سيكون اللغة المعتمدة في نظام التفاضل الشعاعي".
هذا ادعاء كبير قد يؤدي إلى نتائج هامة، فلا يوجد شك في التأثير الكبير لمخططات فاينمان في تغيير طريقة تفكير الفيزيائيين بفيزياء الجسيمات، غير أن التفاضل الشعاعي أكثر امتداداً وتأثيراً، بوصفه الأساس الرياضي للكثير من المجالات الرياضية والهندسية الحديثة.
أما التساؤل الحقيقي فهو مدى الانتشار الذي ستحققه هذه الفكرة، وهو ما سيحدد ما إذا كان الترميز الرسومي سيطلق تحولاً جذرياً في طريقة تفكيرنا بالفيزياء، أو سيقتصر على كونه مجرد ملحوظة هامشية مثيرة للاهتمام في تاريخ الابتكارات الرياضية. وفي كلتا الحالتين، لا شك في أن فاينمان سيكون سعيداً.
المرجع: arxiv.org/abs/1911.00892
تعزيز التفاضل الشعاعي بالترميز الرسومي.