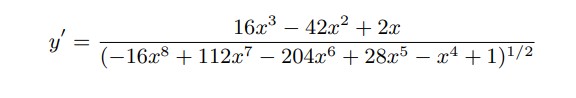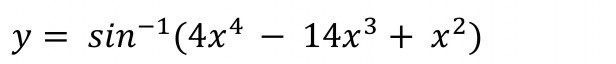نقدم هذا التحدي إلى قرَّائنا من محبيّ الرياضيات، أوجد حلّ المعادلة التفاضلية التالية بالنسبة لـ y خلال 30 ثانية:
هيا، بسرعة! الثواني تمرّ، لا تضيع الوقت!
الجواب بالطبع هو:
إن لم تستطع إيجاد الحل فلا تشعر بالإحباط؛ فالتعبير الرياضي في هذه المعادلة صعبٌ لدرجة أن العديد من حزم البرمجيات الرياضية المتطورة قد فشلَت في هذا التحدي أيضاً، حتى بعد 30 ثانية من إجراء العمليات الحسابية المعقدة على الأرقام.
ولكن اليوم، يقول جويوم لامبل وفرانسوا شارتون من مركز أبحاث فيسبوك للذكاء الاصطناعي في باريس إنهما قد قاما بتطوير خوارزميةٍ يمكنها حلّ هذا التحدي في طرفة عين. لقد نجح هذان الباحثان -للمرة الأولى بهذا المجال- في تدريب شبكةٍ عصبونية على تنفيذ الاستدلال الرمزي اللازم من أجل إجراء عمليات التفاضل والتكامل على التعابير الرياضية. ويعتبر هذا العمل خطوةً هامة نحو تحقيق استدلالٍ رياضي ذو أداءٍ أفضل، كما يمثِّل طريقةً جديدة لتطبيق الشبكات العصبونية على مجالات تتجاوز المهام التقليدية في التعرف على الأنماط. ولنبدأ أولاً ببعض المعلومات الأساسية عن هذا الموضوع.
لقد أصبحت الشبكات العصبونية عاليةَ الكفاءة في مهام التعرف على الأنماط مثل التعرف على الوجوه والأجسام، وفي أنواعٍ معينة من معالجة اللغات الطبيعية، وحتى ممارسة الألعاب مثل الشطرنج ولعبة جو Go وسبيس إنفادرس Space Invaders.
ولكن على الرغم من الجهود الكبيرة، لم يتمكن أحدٌ حتى الآن من تدريب هذه الشبكات على تنفيذ مهام الاستدلال الرمزي من قبيل تلك الموجودة في الرياضيات؛ حيث إن أفضل ما أنجزته الشبكات العصبونية هو إجراء عمليتي الجمع والضرب على الأعداد الصحيحة.
وتتمثل إحدى الصعوبات في التعامل مع التعابير الرياضية المتقدمة -بالنسبة للشبكات العصبونية وللبشر على حدٍّ سواء- في اعتماد هذه التعابير على الاختزال. على سبيل المثال، التعبير الرياضي:
هو طريقةٌ مختزلة لكتابة xمضروبةً في xمضروبةً فيx . وفي هذا المثال فإن “الضرب” بدوره هو اختزالٌ للجمع المتكرر، وهو بحدِّ ذاته اختزالٌ للقيمة الإجمالية لكميتين مجتمعتين.
من السهل أن نلاحظ أن التعابير الرياضية -حتى البسيطة منها- هي توصيفٌ مكثَّف ومُختصَر للغاية لسلسةٍ من عملياتٍ رياضية أكثر بساطة.
لذا فإنه ليس من المستغرب أن تواجه الشبكات العصبونية صعوبةً كبيرة في التعامل مع هذا النوع من المنطق؛ فإذا لم تكن تعلم ما يمثله الاختزال، فلن تملك فرصةً كبيرة في تعلم طريقة استخدامه. وفي الحقيقة، يعاني البشر من نفس المشكلة، وهي غالباً مغروسةٌ فيهم منذ الطفولة.
ومع ذلك، ما زالت عمليات مثل التكامل والتفاضل تنطوي على مهام التعرف على الأنماط على المستوى الأساسي، وإن كانت مخبأةً في الاختزالات الرياضية.
وهنا يتدخَّل الباحثان لامبل وشارتون، اللذان ابتكرا طريقةً رائعة لفكّ الاختزالات الرياضية ونشرها إلى وحداتها الأساسية؛ حيث يقومان بتعليم شبكة عصبونية كيفية التعرف على أنماط التلاعب الرياضية المكافِئة للتكامل والتفاضل. وبعد ذلك يُطلقان العنان للشبكة العصبونية للتعامل مع تعابير رياضية لم تتدرب عليها من قبل، ثم يقارنان النتائج مع الأجوبة التي تم الحصول عليها باستخدام أدوات الحل التقليدية مثل ماثيماتيكا Mathematica وماتلاب Matlab.
ويهدف القسم الأول من طريقتهم إلى تبسيط التعابير الرياضية وتفكيكها إلى الأجزاء المكوِّنة لها، ويقوم لامبل وشارتون بذلك عن طريق تمثيل التعابير على شكل بِنًى شبيهةٍ بالأشجار. وفي هذه الأشجار، الأوراق تمثل الأرقام والثوابت والمتغيرات مثل (x)، أما العقد الداخلية فتمثل العمليات الرياضية مثل الجمع والضرب والمفاضلة بالنسبة لمتغير، وهلمّ جرّاً.
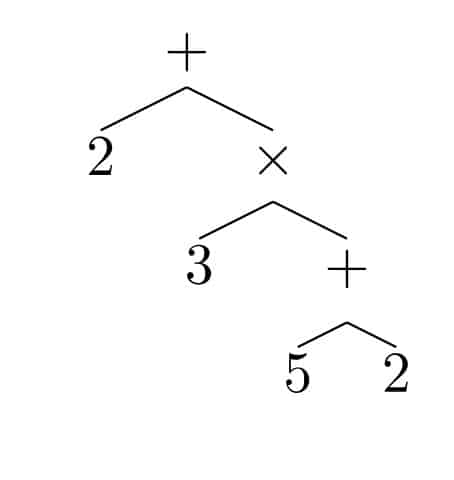
على سبيل المثال، يمكن كتابة التعبير الرياضي:
على الشكل الشَّجَري التالي:
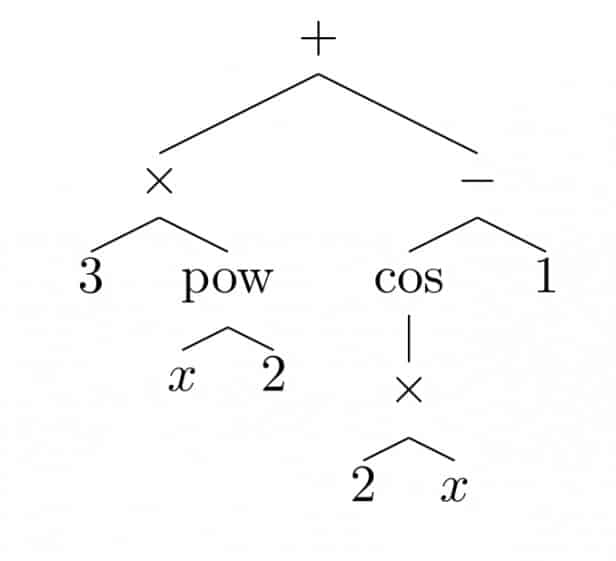
والتعبير الرياضي:
يتم تمثيله على الشكل:
وهكذا دواليك.
وعندما تكون التعابير الرياضية متكافئةً، تكون الأشجار الممثِّلة لها متشابهة. على سبيل المثال:
جميع هذه التعابير متكافئة؛ ولذلك تكون الأشجار الممثلة لها متكافئةً أيضاً.
وعلى هذا النحو، يغدو من السهل التعامل مع الكثير من العمليات الرياضية. يقول لامبل وشارتون: “مثلاً، إن تبسيط التعبير الرياضي هو بمنزلة إيجاد تمثيلٍ مكافئ أقصر طولاً للشجرة”.
كما يمكن كتابة هذه الأشجار على صورة تسلسلات، مع أخذ كل عقدةٍ على التوالي. وعندما توضع بهذا الشكل، تغدو مهيَّأةً للمعالجة بواسطة طريقة شبكات عصبونية تسمى seq2seq.
ومن الجدير بالذكر أنَّ هذه الطريقة كثيراً ما يتم استخدامها في الترجمة الآلية؛ حيث ينبغي ترجمة تسلسلٍ من الكلمات في لغةٍ ما إلى تسلسلٍ من الكلمات المقابلة في لغةٍ أخرى. وفي الواقع، يقول لامبل وشارتون إن طريقتهما تتعامل أساساً مع الرياضيات باعتبارها لغةً طبيعية.
ثم تأتي المرحلة التالية وهي عملية التدريب، التي تتطلب قاعدة بياناتٍ ضخمة من الأمثلة حتى تتعلم الشبكة منها. يقوم لامبل وشارتون بإنشاء قاعدة البيانات هذه عن طريق التجميع العشوائي للتعابير الرياضية انطلاقاً من مكتبةٍ للعمليات الثنائية مثل الجمع والضرب ومثيلاتها، والعمليات الأحادية مثل جيب تمام cos وجيب sin والرفع لقوة exp، بالإضافة إلى مجموعةٍ من المتغيرات والأعداد الصحيحة والثوابت مثل باي π والعدد النيبري e. كما يضع الباحثان حداً أعلى لعدد العقد الداخلية بهدف تجنُّب أن تصبح المعادلات كبيرة جداً.
وحتى مع عددٍ صغير نسبياً من العقد والعناصر الرياضية، فإن عدد التعابير الممكنة كبيرٌ جداً. ثم تتم مكاملة ومفاضلة كلُّ معادلةٍ عشوائية باستخدام نظامٍ حاسوبي للجبر الرياضي، كما يتم تجاهل أيّ تعبيرٍ لا يمكن مكاملته.
وبهذه الطريقة، ينشئ الباحثان مجموعةً ضخمة من بيانات التدريب تتكون، على سبيل المثال، من 80 مليون مثالاً من المعادلات التفاضلية من الدرجتين الأولى والثانية و20 مليون مثالاً لتعابير رياضية تمت مكاملتها بالتجزئة.
ومن خلال التدرب على مجموعة البيانات هذه، تتعلم الشبكة العصبونية كيفية حساب المشتقّ أو التكامل لتعبيرٍ رياضي معطى.
وفي النهاية، يضع لامبل وشارتون شبكتهم العصبونية تحت الاختبار من خلال تزويدها بـ 5000 تعبيرٍ رياضي لم تتدرب عليها من قبل، ثم مقارنة النتائج التي تنتجها في 500 حالة اختبارٍ مع النتائج التي تتوصل إليها أدوات الحل التجارية المتاحة مثل مابل Maple وماتلاب وماثيماتيكا.
وتستخدم هذه الأدوات نهجاً خوارزمياً تم تصميمه في ستينيات القرن الماضي من قِبل عالم الرياضيات الأميركي روبرت ريش. إلا أن خوارزمية ريش ضخمةٌ؛ حيث تصل إلى 100 صفحةٍ من التعامل مع التكامل وحده؛ لذا تلجأ برمجيات الجبر الرمزي إلى استخدام نسخٍ مختصرة منها من أجل تسريع العمليات الحسابية.
إن المقارنة بين أداء هذه الأدوات من جهة وأداء طريقة الشبكة العصبونية من جهةٍ أخرى تكشف الكثير من المعلومات المثيرة للاهتمام. يقول الباحثان: “في جميع المهام التي اختبرناها، وجدنا أن أداء نموذجنا يتفوق على أداء ماثيماتيكا بشكلٍ كبير؛ ففي عمليات التكامل على الدوال، يحقق نموذجنا دقةً تقارب الـ 100%، بينما بالكاد تصل دقة ماثيماتيكا إلى 85%”. أما حزم مابل وماتلاب فهي تحقق- بالمتوسط- دقةً أدنى من دقة ماثيماتيكا.
وفي الكثير من الحالات، يتعذَّر على الأدوات التقليدية إيجاد حلٍّ على الإطلاق عند منحها 30 ثانية فقط. وبالمقارنة، تستغرق الشبكة العصبونية حوالي الثانية لإيجاد الحلول. وكان المثال في مستهلّ المقال أحدَ هذه الحالات.
وكانت إحدى النتائج المثيرة للاهتمام هي أن الشبكة العصبونية غالباً ما وجدت عدة حلولٍ متكافئة لنفس المشكلة. وهذا يعود إلى أن التعابير الرياضية يمكن عادةً كتابتها بعدة طرقٍ مختلفة.
وهذه القدرة هي لغزٌ محيِّر للباحثَين؛ حيث يقول لامبل وشارتون: “إن قدرة نموذجنا على استنباط تعابير متكافئة دون تدريبه على القيام بذلك، هو أمر مثيرٌ للاهتمام”.
وتعتبر هذه الطريقة إنجازاً غير مسبوق؛ حيث يقول الباحثان: “على حدِّ معرفتنا، لم تقم أية دراسةٍ سابقة بالتحري عن قدرة الشبكات العصبونية على اكتشاف الأنماط في التعابير الرياضية”.
والآن بعد أن قاما بذلك، من الواضح أن النتيجة تَعِد بإمكاناتٍ كبيرة في مجالٍ تتزايد أهميته وتعقيده باستمرار: ألا وهو مجال الرياضيات الحاسوبية.
ولم يكشف الباحثان عن خطط فيسبوك المستقبلية في استخدام طريقتهما الجديدة؛ لكن من السهل توقع إمكانية تقديمها لخدمة الجبر الرمزي الخاصة بها، التي تتفوق على الرواد المهيمنين على هذه السوق.
ولكن، من غير المرجح أن يقف المنافسون مكتوفي الأيدي؛ إذ نتوقع نشوب منافسةٍ حامية الوطيس في عالَم الرياضيات الحاسوبية.
المرجع: arxiv.org/abs/1912.01412
التعلم العميق في الرياضيات الرمزية.