في القرن الثامن عشر، كان أحد أكبر التحديات العلمية في ذلك العصر إيجاد وسيلة تتيح للبحّارة تحديد موضعهم في البحر، وكان أحد أنجح الحلول هو قياس موضع القمر في السماء بالنسبة إلى الخلفية الثابتة المليئة بالنجوم. وبسبب تأثيرات التزيّح Parallax (أي اختلاف المنظر بسبب تغير زاوية النظر)، فإن هذا القياس يعتمد على موضع القائس، وبمقارنة الموضع المحسوب مع جدول من المواضع المحسوبة بالنسبة لمراقب في جرينتش بإنجلترا، يستطيع البحّار تحديد خط الطول الذي يقع عليه.
ولكن كانت هناك مشكلة واحدة، هي أن حساب موضع القمر مسبقاً أمر أصعب مما قد نعتقد؛ لأن الشمس تؤثر بقوة ثقالية صغيرة ولكن واضحة على القمر، وهو ما يجعل من حركة الأرض والقمر والشمس مسألة أجسام ثلاثة، وهي مسألة أخفق الكثير من الرياضيين في حلها على مر التاريخ.
تكمن صعوبة هذه الحركة ثلاثية الأجسام في أنها عشوائية إلا في بعض الحالات الخاصة. ولهذا، لا توجد وسيلة سهلة للتنبؤ بمواضعها في المستقبل، وهو ما أدى إلى وجود أخطاء في جداول الملاحة القمرية، ونتائج تفتقر إلى الدقة، بل تكون مدمرة في بعض الأحيان.
غير أن البحارة استفادوا من هذه الطريقة المشوبة بالأخطاء قدر الإمكان حتى منتصف القرن التاسع عشر، عندما أصبحت الساعات رخيصة ودقيقة بما يكفي لاستخدامها على نطاق واسع في السفن. وفي نهاية المطاف، أصبحت طريقة الساعة، التي اشتُهر جون هاريسون بريادتها، الطريقة المفضلة لحساب خط الطول.
ولكن مسألة الأجسام الثلاثة لم تتوقف عن مطاردة الرياضيين كالشبح. وقد تحولت الآن إلى مسألة تحديد بنية مجموعات النجوم الكروية والنوى المجرّية، التي تعتمد على طريقة تفاعل الأنظمة الثنائية من الثقوب السوداء مع الثقوب السوداء المنفردة.
وفي نهاية المطاف، وبعد ظهور الحواسيب ذات القدرات الكبيرة، تمكن الرياضيون من تحديد مواضع الثقوب السوداء بفضل الحسابات التكرارية. ولكن ذلك يتطلب موارد حاسوبية هائلة، بل إن بعض الحلول بقيت خارج نطاق قدرات تلك الحواسيب، ولهذا توجد حاجة ماسّة لطريقة أكثر فعالية لحل مسألة الأجسام الثلاثة.
وهنا يأتي دور فيليب برين في جامعة إدنبره مع مجموعة من زملائه، حيث قاموا بتدريب شبكة عصبونية على حساب هذه الحلول. وأهم ناحية في هذا الإنجاز هو أن الشبكة قادرة على تقديم حلول دقيقة بتكلفة حاسوبية ثابتة وأسرع من أحدث أنظمة الحل التقليدية بما يصل إلى مائة مليون مرة.
بدأ الباحثون بطريقة تدريب نموذجية للشبكات العصبونية، وهو ما يتطلب قاعدة بيانات من مسائل الأجسام الثلاثة مع الحلول المحسوبة باستخدام نظام حل حديث للغاية.
قام برين وزملاؤه أولاً بتبسيط المسألة بحدّها بثلاثة جسيمات متساوية الكتلة على سطح مستوٍ بسرعة ابتدائية تساوي الصفر، وقاموا باختيار المواضع الابتدائية عشوائياً وحل المسألة باستخدام طريقة حل حديثة تسمى بروتوس، ومن ثم كرروا هذه العملية 100,000 مرة.
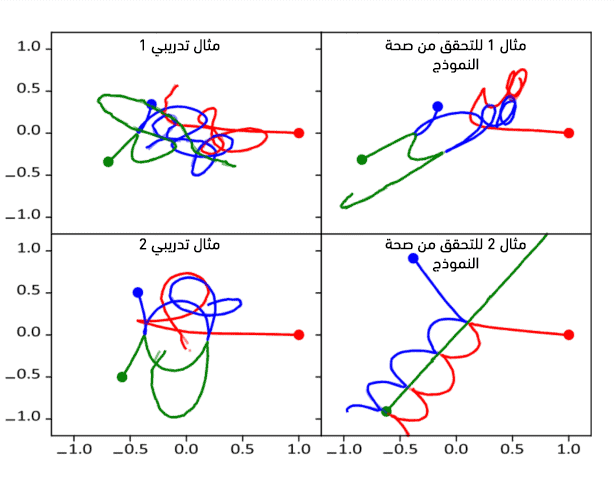
استخدم الفريق 9,900 مثال لتدريب الشبكة العصبونية و100 مثال للتأكد من صحة عملها، وقاموا أخيراً باختبار الشبكة باستخدام 5,000 تموضع جديد كلياً ومقارنة التوقعات مع نتائج حسابات بروتوس.
وقد توصل الباحثون إلى نتائج مثيرة للاهتمام؛ فقد تمكنت الشبكة العصبونية من التنبؤ بحركة الأجسام الثلاثة في المستقبل بدقة، وعلى وجه الخصوص، تمكنت من محاكاة التباعد بين المسارات المتقاربة بشكل يشابه إلى حد بعيد محاكاة بروتوس. يقول برين وزملاؤه: "لقد بيَّنَّا أن الشبكات العصبونية الاصطناعية العميقة تنتج حلولاً سريعة ودقيقة لمسألة الأجسام الثلاثة التي تُعتبر من المسائل الصعبة حاسوبياً، وذلك خلال فترة زمنية ثابتة".
إضافة إلى ذلك، فقد اختبر الباحثون توقعات الشبكة العصبونية بدراسة مدى توفيرها للطاقة، وبعد بضعة تعديلات، حققت الشبكة شروط توفير الطاقة بخطأ لا يتجاوز واحداً من مائة ألف.
هذا عمل مثير للإعجاب وقد يؤدي إلى نتائج هامة، خصوصاً وأن الباحثين ذكروا أن الشبكة العصبونية يمكن أن تساعد على حل مسائل الأجسام الثلاثة التي أصبحت مستحيلة بالنسبة لبروتوس.
إذن فإن رؤيتهم تقوم على بناء نظام هجين، وفي هذه الحالة سيتولى بروتوس النسبة العظمى من العمل، ولكن عندما يصبح العبء الحاسوبي كبيراً للغاية، فستتدخل الشبكة العصبونية حتى تصبح المسألة قابلة للحل مرة أخرى. وبهذا ستصبح محاكاة حركة الأجسام السوداء ضمن النوى المجرّيّة ومجموعات النجوم الكروية أكثر دقة من ذي قبل بفضل الشبكات العصبونية.
هذه ليست سوى البداية. يقول الباحثون: "في نهاية المطاف، قد يتم تدريب هذه الشبكة على مسائل أكثر عشوائية، مثل مسائل أربعة أو خمسة أجسام، مما يخفف العبء على الحاسوب إلى درجة أكبر".
المرجع: arxiv.org/abs/1910.07291:
نيوتن ضد الآلة: حل مسألة الأجسام الثلاثة العشوائية باستخدام الشبكات العصبونية العميقة.