ما لم تكن فيزيائياً أو مهندساً، فليس هناك الكثير من الأسباب التي تجعلك مطلعاً على المعادلات التفاضلية الجزئية. أنا أعلم ذلك؛ فبعد سنوات من التأمل فيها في المرحلة الجامعية أثناء دراستي الهندسة الميكانيكية، لم أستخدمها مطلقاً منذ ذلك الحين في العالم الحقيقي.
لكن المعادلات التفاضلية الجزئية (PDEs) تتمتع بنوع من السحر؛ فهي تمثل فئة من المعادلات الرياضية التي تعد جيدة حقاً في وصف التغيير عبر المكان والزمان، وبالتالي فهي مفيدة جداً في توصيف الظواهر الفيزيائية في كوننا. ويمكن استخدامها لنمذجة كل شيء من مدارات الكواكب إلى الصفائح التكتونية إلى اضطراب الهواء الذي يزعج الرحلة، وهذا بدوره يسمح لنا بالقيام بأشياء عملية مثل التنبؤ بالنشاط الزلزالي وتصميم طائرات آمنة.
تكمن المشكلة في صعوبة حلّ المعادلات التفاضلية الجزئية. وفي هذا الصدد، ربما من الأفضل تقديم مثال لتوضيح معنى “حلّ” هذه المعادلات. لنفترض أنك تحاول محاكاة الاضطرابات الجوية لاختبار تصميم جديد للطائرة. هناك معادلة تفاضلية جزئية معروفة تسمى نافييه-ستوكس تستخدم لوصف حركة أي سائل. ويتيح لك “حل” معادلة نافييه-ستوكس أخذ لمحة عن حركة الهواء (مثل ظروف الرياح) في أي وقت ونمذجة كيفية استمراره في الحركة، أو كيفية حركته في وقت سابق.
غير أنّ هذه الحسابات معقدة للغاية ومكلفة من الناحية الحاسوبية، ولهذا السبب غالباً ما تعتمد التخصصات التي تستخدم الكثير من المعادلات التفاضلية الجزئية على الحواسيب الفائقة لإجراء العمليات الحسابية. وهذا ما يفسِّر أيضاً الاهتمام الخاص الذي يوليه مجال الذكاء الاصطناعي بهذه المعادلات؛ فإذا ما تمكنا من استخدام التعلم العميق لتسريع عملية حلها، فيمكن لهذا الأمر أن يحمل فائدة عظيمة للبحث العلمي والهندسة.
وحالياً، قام باحثون في معهد كاليفورنيا للتكنولوجيا بتقديم تقنية تعلم عميق جديدة لحل المعادلات التفاضلية الجزئية على نحو أكثر دقة بكثير من أساليب التعلم العميق التي تم تطويرها سابقاً. كما تتمتع التقنية الجديدة بأنها أكثر قابلية للتعميم، وقادرة على حل مجموعات كاملة من المعادلات التفاضلية الجزئية (مثل معادلة نافييه-ستوكس لأي نوع من السوائل) دون الحاجة إلى إعادة التدريب. أخيراً، تتميز التقنية الجديدة بأنها أسرع 1,000 مرة من الصيغ الرياضية التقليدية، ما يخفف من اعتمادنا على الحواسيب الفائقة ويزيد قدرتنا الحاسوبية على نمذجة مشاكل أكبر. هذا صحيح، لنَخُض أكثر في التفاصيل.
مغني الراب إم سي هامر مهتم أيضاً بالتقنية الجديدة
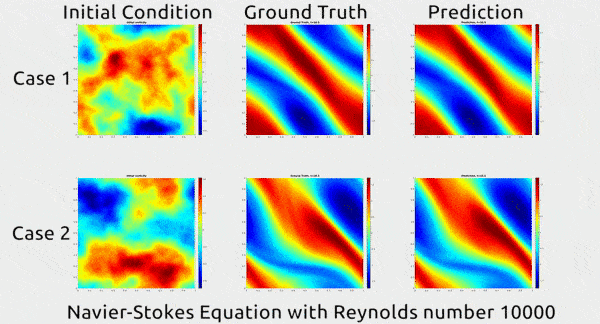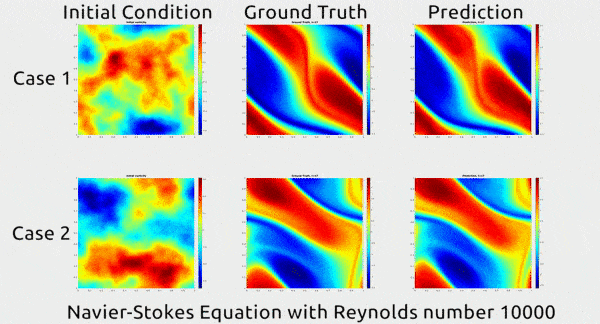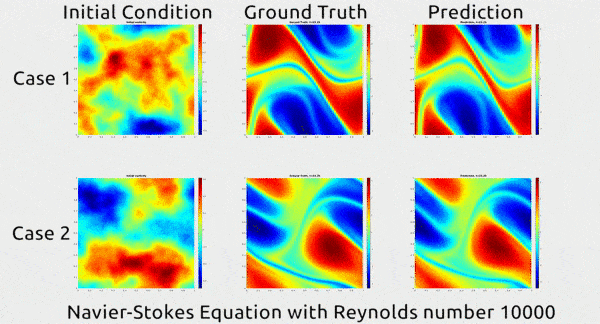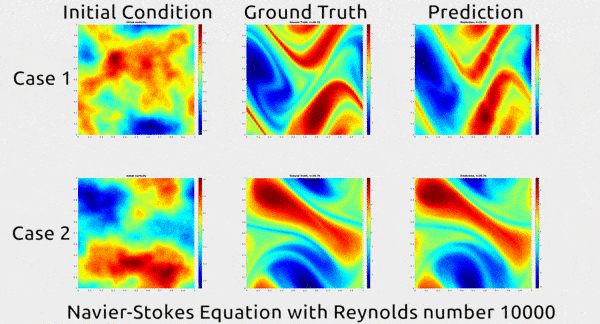
قبل أن نتعمق في كيفية قيام الباحثين بتطوير التقنية الجديدة، دعونا أولاً نتفهم النتائج. في الصورة المتحركة أدناه، يمكنك رؤية توضيح مثير للإعجاب. يُظهر العمود الأول لقطتين لحركة السائل؛ أما الثاني فيوضِّح كيف استمر السائل في التحرك ضمن بيئة حقيقية؛ والثالث يوضح كيف توقعت الشبكة العصبونية ما ستكون عليه حركة السائل. يبدو التوقع متطابقاً تقريباً مع حركة السائل في أرض الواقع.
نالت الورقة البحثية الكثير من الجلبة على تويتر، وحتى حظيت بمشاركة من مغني الراب إم سي هامر. نعم ودون مزاح!
Fourier Neural Operator for Parametric Partial Differential Equations #Hamm400aos https://t.co/ABYRwadcT7
— MC HAMMER (@MCHammer) October 22, 2020
حسناً، لنعد الآن إلى توضيح كيفية نجاحهم في ذلك.
عندما يكون التابع مناسباً
بادئ ذي بدء، لا بدّ من فهم أن الشبكات العصبونية هي في جوهرها عبارة عن أداة تقريبية للتوابع. (تقريبية؟!) عندما يتم تدريبها على مجموعة بيانات من المدخلات والمخرجات المقترنة بها، فإنها في الواقع تقوم بحساب التابع، أو سلسلة من العمليات الرياضية، التي تتحول من عملية إلى أخرى. ولتقريب الفكرة أكثر، فكر في بناء جهاز تمييز صور القطط. أنت تدرب الشبكة العصبونية عن طريق تزويدها بالكثير من صور القطط والأشياء الأخرى غير القطط (المدخلات) ووسم كل مجموعة بـ 1 أو 0، على التوالي (المخرجات). تبحث الشبكة العصبونية بعد ذلك عن أفضل تابع يمكنه تحويل كل صورة قطة إلى 1 وكل صورة لأي شيء آخر إلى 0. هذه هي الطريقة التي تمكن الشبكة العصبونية من دراسة صورة جديدة وإخبارك بما إذا كانت صورة قطة أم لا. إنها تستخدم التابع الذي اكتشفته لحساب إجابتها، وإذا كان تدريبها جيداً، فإنها ستعطيك الإجابة الصحيحة في معظم الأوقات.
وبكل بساطة، فإن عملية تقريب التابع هذه هي ما نحتاجه لحل المعادلات التفاضلية الجزئية. ففي نهاية المطاف، نحن نحاول العثور على تابع يستطيع أن يقدم أفضل توصيف، على سبيل المثال، لحركة جسيمات الهواء عبر الفضاء والزمان الماديين.
هذا هو جوهر الورقة البحثية. عادة ما يتم تدريب الشبكات العصبونية لتقريب التوابع بين المدخلات والمخرجات المحددة في الفضاء الإقليدي، أي الرسم البياني التقليدي الذي يتضمن محاور x وy وz. لكن هذه المرة، قرر الباحثون تحديد المدخلات والمخرجات في فضاء فورييه، وهو نوع خاص من الرسم البياني المخصص لرسم الترددات الموجية.
تقول أنيما أناندكومار، الأستاذة في معهد كاليفورنيا للتكنولوجيا والتي أشرفت على البحث جنباً إلى جنب مع زملائها الأستاذين أندرو ستيوارت وكاوشيك بهاتاشاريا، إن الحدس الذي استفادوا منه من العمل في مجالات أخرى هو أنه يمكن توصيف شيء مثل حركة الهواء على أنه مزيج من ترددات الموجات. ويمكن تشبيه الاتجاه العام للرياح على المستوى الكلي بالتردد المنخفض لموجات طويلة جداً وخاملة، في حين أن الدوامات الصغيرة التي تتشكل على المستوى الجزئي تشبه الترددات العالية للموجات القصيرة جداً والسريعة.
لماذا يعد ذلك مهماً؟ يكمن السبب في أنه من الأسهل بكثير تقريب تابع فورييه في فضاء فورييه بدلاً من الخوض مع المعادلات التفاضلية الجزئية في الفضاء الإقليدي، ما يبسط عمل الشبكة العصبونية إلى حد كبير. وعلاوة على ميزة السرعة الهائلة التي تتمتع بها التقنية الجديدة مقارنة بالأساليب التقليدية، فإنها تحقق معدل خطأ أقل بنسبة 30% عند حل نافييه-ستوكس مقارنةً بأساليب التعلم العميق السابقة. وهو ما يمثل إشارة إلى مكاسب الدقة والكفاءة التي توفرها.
تعد التقنية الجديدة بكل تفاصيلها غاية في الذكاء، كما أنها تجعل من أسلوب الحل أكثر قابلية للتعميم؛ إذ كان ينبغي تدريب أساليب التعلم العميق السابقة بشكل منفصل لكل نوع من السوائل، في حين أن هذه الطريقة تحتاج فقط إلى التدريب مرة واحدة للتعامل معها جميعاً، وفق ما أكدته تجارب الباحثين. وعلى الرغم من أنهم لم يحاولوا بعد توسيع التقنية لتشمل أمثلة أخرى، إلا أنه من المفترض أن تتمكن من التعامل مع جميع التركيبات الأرضية عند حل المعادلات التفاضلية الجزئية المتعلقة بالنشاط الزلزالي، أو مع كل أنواع المواد عند حل المعادلات التفاضلية الجزئية المتعلقة بالتوصيل الحراري.
محاكاة فائقة
لم يقم الأساتذة وطلاب الدكتوراه بهذا البحث لمجرد التسلية النظرية، وإنما قاموا بذلك في سعيٍ منهم لإدخال الذكاء الاصطناعي إلى المزيد من التخصصات العلمية. ومن خلال التحدث إلى العديد من المتعاونين في علوم المناخ وعلم الزلازل وعلوم المواد، قررت أناندكومار أولاً التصدي لتحدي حل المعادلات التفاضلية الجزئية مع زملائها وطلابها. إنهم يعملون الآن على وضع طريقتهم موضع التنفيذ مع باحثين آخرين في معهد كاليفورنيا للتكنولوجيا ومختبر لورانس بيركلي الوطني.
ويتمثل أحد الموضوعات البحثية التي تثير اهتمام أناندكومار بشكل خاص في تغير المناخ؛ إذ لا تقتصر فائدة معادلات نافييه-ستوكس في قدرتها على نمذجة الاضطراب الجوي، بل تستخدم أيضاً في نمذجة الأنماط المناخية. وتقول أناندكومار: “إن توافر تنبؤات جيدة ودقيقة بالطقس على نطاق عالمي يمثل مشكلة صعبة للغاية، وحتى باستخدام أضخم الحواسيب الفائقة لا يمكننا القيام بذلك على نطاق عالمي اليوم. لذلك إذا تمكنا من استخدام هذه الأساليب لتسريع العملية برمتها، فسيكون لهذا الأمر تأثير هائل”.
وتضيف أن هناك أيضاً الكثير من التطبيقات الأخرى لهذه التقنية. وتختم قائلة: “بهذا المعنى، لا حدود لاستخدامات هذه التقنية، لأنها تمثل طريقة عامة لتسريع جميع هذه التطبيقات”.